Задача нахождения кратчайшего пути является, пожалуй, наиболее важной задачей теории графов. Существует множество алгоритмов поиска как кратчайших, оптимальных путей, так и субоптимальных путей. Субоптимальным путём будем называть путь, ведущий из начальной в конечную точку, но отличающийся от оптимального пути. Смысл нахождения субоптимальных путей легко рассмотреть на таком примере: предположим, что задача поиска пути напрямую описывает наш путь по городу. В таком случае оптимальный путь в зависимости от времени может оказаться невозможным к реализации (например, одна из ветвей дороги перегорожена пробкой из-за аварии). В таком случае нас будет интересовать субоптимальный путь, или по-другому, объезд.
Решение задачи поиска оптимального пути мы проведём по алгоритму Флойда, субоптимальные пути найдём по алгоритму Иена.
Алгоритм Флойда
Алгоритм Флойда — Уоршелла — динамический алгоритм для нахождения кратчайших расстояний между всеми вершинами взвешенного ориентированного графа. Разработан в 1962 году Робертом Флойдом и Стивеном Уоршеллом
Описание алгоритма
Пусть вершины графа 
пронумерованы от 1 до n и введено обозначение 
для длины кратчайшего пути от i до j, который кроме самих вершин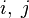 
проходит только через вершины 
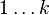. Очевидно, что 
— длина (вес) ребра 
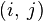, если таковое существует (в противном случае его длина может быть обозначена как 
)
Существует два варианта значения 
:
- Кратчайший путь между 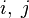не проходит через вершину k, тогда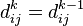
- Существует более короткий путь между 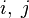, проходящий через k, тогда он сначала идёт от i до k, а потом от k до j. В этом случае, очевидно,
Таким образом, для нахождения значения функции достаточно выбрать минимум из двух обозначенных значений.
Тогда рекуррентная формула для 
имеет вид:
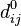— длина ребра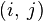
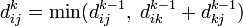
Алгоритм Флойда — Уоршелла последовательно вычисляет все значения , 
для k от 1 до n. Полученные значения 
являются длинами кратчайших путей между вершинами .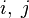
Псевдокод
На каждом шаге алгоритм генерирует двумерную матрицу W,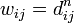 
. Матрица W содержит длины кратчайших путей между всеми вершинами графа. Перед работой алгоритма матрица W заполняется длинами рёбер графа.
for k = 1 to n
for i = 1 to n
for j = 1 to n
W[i][j] = min(W[i][j], W[i][k] + W[k][j])
Сложность алгоритма
Три вложенных цикла содержат операцию, исполняемую за константное время. 
то есть алгоритм имеет кубическую сложность, при этом простым расширением можно получить также информацию о кратчайших путях — помимо расстояния между двумя узлами записывать матрицу идентификатор первого узла в пути.
Построение матрицы достижимости
Алгоритм Флойда — Уоршелла может быть использован для нахождения замыкания отношения E по транзитивности. Для этого в качестве W[0] используется бинарная матрица смежности графа,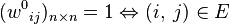 
; оператор min заменяется дизъюнкцией, сложение заменяется конъюнкцией:
for k = 1 to n
for i = 1 to n
for j = 1 to n
W[i][j] = W[i][j] or (W[i][k] and W[k][j])
После выполнения алгоритма матрица W является матрицей достижимости.
Алгоритм Йена
Нахождение k кратчайших путей в графе
Есть неориентированный граф. Состоит из вершин и ребер, ребрам приписаны длины. Вершин несколько тысяч (N штук), количество ребер известно (M штук). Дополнительных сведений о соотношении числа ребер и числа вершин нет.
Надо найти несколько кратчайших путей без циклов между двумя заданными точками (K штук путей, K задается, K порядка нескольких десятков)
Суть алгоритма
Позволяет находить k-кратчайшие пути без циклов последовательно.
Этот алгоритм предполагает, что мы умеем находить один кратчайший путь в графе.
Делается это так: Будем вести список кандидатов в кратчайшие пути. Находится первый кратчайший путь. Так как все другие пути не должны совпадать с первым путем, то эти остальные пути не содержат как минимум одно из ребер первого пути. Поэтому, выкидываем по одному ребру из первого пути и находим кратчайшие пути в получаемых графах. Найденные пути (с пометкой о том, какое ребро было выкинуто) добавляем в список кандидатов. Из списка кандидатов выбираем самый короткий путь — это второй самый короткий путь.
Далее находим следующий самый короткий путь аналогично. При нахождении каждого самого короткого пути в список кандидатов добавляется не более N новых путей (на самом деле конечно меньше).
При удалении ребра нахождение кратчайшего пути в полученном графе производится вроде за линейное время. Для этого в исходном графе алгоритм Дейкстры запускается как от начальной, так и от конечной вершины. При удалении одного ребра кратчайший путь в новом графе ищется с использованием деревьев, полученных для исходного графа.
Модификация алгоритма Йена
За счет того, что граф не ориентирован, при нахождении каждого самого короткого пути в список кандидатов добавляется максимум три новых пути.
Реализация
Попытаемся реализовать оба алгоритма на языке C++ с демонстрацией решения в консольном приложении. Наши решатели будут работать с матрицей весов путей графа. В такой матрице каждая ячейка показывает вес ребра в ориентированном графе. Алгоритм может также принимать на вход граф, имеющий рёбра с отрицательным весом.
Для удобной работы с матрицами мы будем использовать удобный класс для работы с динамическими многомерными массивами. Рассмотрим этот класс поближе.
Класс array
Сам класс описывается следующей конструкцией:
class c_array {
private :
int dimentions; // Nubmer Of Dimentions
int *size; // Array Of Sizez-By-Dimention
int *coords; // Array Of Coords-By-Dimention
int length; // Total Length
int *data; // Pointer to Data
int id (); // Getting The ID
public:
// Initialization
c_array (int dimentions, int size, ...); // Creating the Array
c_array (int dimentions, int *size, int *data); // Creating the Array from Clone
c_array (char * path); // Creating the Array from File
~c_array (); // Cleaning Up Memory
// Misc
c_array_p clone (); // Clone the Array
int save(char * path); // Save Data to File
// Data
int $ (int coords, ...); // Gets the Value
int s (int value, int coords, ...); // Sets the Value
int l (int dimention); // Get Lenght by Dimention
};
Поля этого класса отвечают за данные нашего массива. Мы указываем количество измерений массива, создаём два массива, хранящих размерности массива по каждому из измерений и координаты запрашиваемой точки, общую длину массива данных и ссылку на сам массив.
Для этого класса предусмотрено три различных типа конструкторов. Основной вариант предполагает создание массива по количеству его измерений и размерностям по каждому из измерений. Второй вариант создаёт массив на базе уже существующего, используя ссылки на его данные. Третий тип конструктора позволяет загрузить массив из файла.
Рассмотрим подробнее основной конструктор:
c_array :: c_array(int dimentions, int size, ...) {
this->dimentions = dimentions;
this->length = size;
this->size = (int*) malloc (sizeof(int) * dimentions);
this->coords = (int*) malloc (sizeof(int) * dimentions);
va_list argp;
this->size[0] = size;
va_start (argp, size);
for (int i = 1; i < dimentions; i++) {
this->size[i] = va_arg (argp, int);
this->length *= this->size[i] ;
}
va_end (argp);
this->data = (int*) malloc (sizeof(int) * this->length);
}
Работа данного конструктора элементарна. Мы заполняем поле количества измерений по переданному первому параметру функции и выделяем место в памяти под два массива – массив размерностей по измерениям и массив координат точки. Далее, используя макросы функций с множественными параметрами, мы заполняем массив размерностей, подсчитывая также в цикле и общую длину массива. Заполним массив размерностей, мы получаем полную длину массива, на основе которой выделяем память под область данных массива.
Для работы с алгоритма Флойда нам потребуется клонирование массивов. Для этого мы используем простую функцию clone и конструктор клонирования.
c_array_p c_array :: clone () {
return new c_array (this->dimentions, this->size, this->data);
}
Конструктор клонирования копирует данные из памяти по переданным в аргументе адресам.
c_array::c_array (int dimentions, int *size, int *data) {
this->dimentions = dimentions;
this->length = 1;
this->size = (int*) malloc (sizeof(int) * dimentions);
this->coords = (int*) malloc (sizeof(int) * dimentions);
for (int i = 0; i < dimentions; i++) {
this->size[i] = size[i];
this->length *= size[i];
}
this->data = (int*) malloc (sizeof(int) * this->length);
for (int i = 0; i < this->length; i++) {
this->data[i] = data[i];
}
}
Для получения и сохранения данных используются две функции — $ и s соответственно. Реализация этих функций в целом очень схожа – заполняется массив координат из переданных аргументов, получается идентификатор ячейки массива по данным координатам и в зависимости от идентификатора функция возвращает или устанавливает значение ячейки, или же возвещает об ошибке переданных координат.
Функция получения значения:
int c_array :: $ (int coords, ...) {
va_list argp;
this->coords[0] = coords;
va_start (argp, coords);
for (int i = 1; i < dimentions; i++) {
this->coords[i] = va_arg (argp, int);
}
va_end (argp);
int id = this->id ();
return (id != -1) ? this->data[id] : -1;
}
Функция установки значения ячейки:
int c_array :: s (int value, int coords, ...) {
va_list argp;
this->coords[0] = coords;
va_start (argp, coords);
for (int i = 1; i < dimentions; i++) {
this->coords[i] = va_arg (argp, int);
}
va_end (argp);
int id = this->id ();
if (id != -1) {
this->data[id] = value;
return true;
} else return false;
}
Обе функции обращаются к функции id, которая проверяет координаты ячейки и возвращает её идентификатор.
int c_array :: id () {
int num = 1;
for (int i = 0; i < this->dimentions; i++) {
if (this->coords[i] >= this->size[i]) {
num = 0;
break;
}
}
if (num) {
switch (this->dimentions) {
case 1:
return this->coords[0];
case 2:
return this->coords[0] + (this->coords[1] * this->size[0]);
case 3:
return this->coords[0] + (this->coords[2] * this->size[1]) + (this->coords[1] * (this->size[0] * this->size[1]));
default:
for (int i = 1; i < this->dimentions; i++) {
int mult = 1;
for (int j = 0; j < this->dimentions - i; j++) {
mult *= this->size[j];
}
num += this->coords[i] * mult;
}
num += this->coords[0];
return num;
}
} else return -1;
}
Как мы видим, функция прежде всего проверяет переданные в неё координаты на соответствие размерностям массива. Далее, в зависимости от количества измерений, идентификатор находится по простым формулам, или же используется сложная формула поиска идентификатора для многомерных массивов.
Дополнительно, мы реализовали функции сохранения и загрузки массивов. Функция сохранения позволяет записать все данные массива в определённый файл. Из него с помощью конструктора третьего типа можно загрузить данные в массив. Ознакомиться с ними можно в файле array.cpp, их реализация элементарна и рассматривать их здесь мы не будем.
Класс floyd и реализация алгоритма
Основная часть алгоритма реализована в классе решателя c_floyd.
typedef class c_floyd {
private:
// Main Graph
c_array_p graph;
// Path Data
c_array_p waypoints;
int path_count;
path_p paths;
// Commmons
int reset_floyd ();
public:
c_floyd ();
~c_floyd ();
// Graph Operations
int graph_init (int vertexes);
int graph_rand ();
int graph_set (int a, int b, int weight);
int graph_clear (int a, int b);
int graph_load (char *path);
int graph_save (char *path);
int graph_print ();
// Floyd Operations
int floyd (int a, int b);
path_p path (int id);
int way_print ();
int path_print (int id = -1);
} c_floyd_t, *c_floyd_p;
Поля этого класса содержат в себе основные данные, используемые в алгоритме. Прежде всего, мы используем массив, описывающий граф – как не сложно догадаться, это поле graph.
Для описания найденных путей используется матрица точек пути waypoints, показывающая, в какую точку лучше перейти, чтобы попасть из точки А в точку Б, количество найденных путей path_count и, собственно, массив найденных путей paths.
Текущее состояние системы, найденные пути и путевые точки, сбрасываются при помощи функции reset_floyd, которая очищает память от найденных ранее путей. Эта функция вызывается при любом изменении графа, т.к. в случае изменения графа пути, как правило, становятся неактуальными.
Для описания найденных нами путей воспользуемся структурой путь.
typedef struct _path {
int type;
int length;
int weight;
int *points;
} path_t, *path_p;
Она содержит в себе тип пути (оптимальный обозначаем как ноль, субоптимальный помечаем единицей), количество точек в пути, его вес и ссылку на массив точек пути.
Конструктор и деструктор класса работают только на выделение и освобождение памяти, рассматривать из здесь подробно не имеет смысла.
Для работы с самим графом мы используем некоторый набор функций, позволяющих легко установить все его параметры.
Прежде всего, граф создаётся функцией graph_init.
int c_floyd :: graph_init (int vertexes) {
if (this->graph) {
delete this->graph;
this->graph = null;
}
this->graph = new c_array (2, vertexes, vertexes);
for (int i = 0; i < vertexes; i++) {
for (int j = 0; j < vertexes; j++) {
this->graph->s (0, i, j);
}
}
this->reset_floyd ();
return true;
}
В её задачи входит очистка предыдущего графа, если таковой имеется, выделение места под новый объект графа и заполнение его нулями.
Для работы с уже существующими графами мы можем использовать функции загрузки и сохранения графов. Они вызывают напрямую функции загрузки и сохранения массива из класса графа, реализацию их можете рассмотреть в самом файле.
В работе нам может понадобиться редактирование весов рёбер графа. Для этого используются две функции: graph_set и graph_clear. Функция graph_set задаёт значение веса ребра между вершинами A и B в переданное значение. Функция graph_clear убирает ребро между этими точками, устанавливая расстояние между ними в бесконечность.
int c_floyd :: graph_set (int a, int b, int weight) {
if (this->graph) {
this->graph->s (weight, a, b);
this->reset_floyd ();
return true;
} else return false;
}
int c_floyd :: graph_clear (int a, int b) {
if (this->graph) {
this->graph->s (inf, a, b);
this->reset_floyd ();
return true;
} else return false;
}
В нашем случае бесконечность, разумеется, не является истиной бесконечностью, мы используем константу inf с достаточно большим значением 0x0fffffff. Мы не используем значение MAX_INT потому, что нам требуется в некоторых случаях складывать значения весов двух рёбер бесконечной длины, и в случае использования MAX_INT возникают ошибки.
Чтобы не задавать значения весов рёбер вручную, используем функцию graph_rand.
int c_floyd ::graph_rand() {
if (this->graph) {
int l = this->graph->l (0);
for (int i = 0; i < l; i++) {
for (int j = 0; j < l; j++) {
if (i != j) {
int w = (rand()%2) ? (rand() % 20 + 1) : inf;
this->graph->s (w, i, j);
} else this->graph->s (inf, i, j);
}
}
this->reset_floyd ();
return true;
} else return false;
}
Она заполняет граф случайными значениями.
Дополнительно, имеется функция graph_print, которая распечатывает граф в консоли. Она выводит на экран матрицу весов рёбер графа.
Решатель – функция floyd
Основная логика работы алгоритма реализована в функции floyd, которая получает на вход номера вершин A и B, и выдаёт ответом количество найденных ей путей.
Начинается наша функция здесь …
int c_floyd::floyd(int a, int b) {
if (! this->graph) return false;
this->reset_floyd ();
int l = this->graph->l(0);
if (a < 0 || a > l) return false;
if (b < 0 || b > l) return false;
Начало функции отвечает за минимальную подготовку к работе алгоритма. Мы очищаем память и проверяем, входят ли требуемые точки в заданный нами диапазон размеров графа.
this->waypoints = new c_array (2, l, l);
for (int i = 0; i < l; i++) {
for (int j = 0; j < l; j++) {
this->waypoints->s (j, i, j);
}
}
Перед запуском алгоритма мы должны подготовить матрицу точек пути, которую мы заполняем для начала конечными точками маршрута.
c_array_p old_step, new_step, temp_step; old_step = new c_array (2, l, l); new_step = this->graph->clone ();
Для работы нам потребуются две матрицы, которые используются при нахождении весов кратчайших путей. Первую мы клонируем из графа, вторую создаём аналогичного размера, но не заполняя данными.
Алгоримт работает в трёх вложенных циклах, как и описано выше. Перед каждым из циклов мы меняем матрицы местами, и продолжаем заполнение.
Каждый раз элемент матрицы устанавливается в значение кратчайшего пути из данной точки в требуемую точку. При этом, если новое значение лучше, чем текущее, текущее значение заменяется. В этом случае также меняется матрица точек пути, см. #1.
for (int k = 0; k < l; k++) {
// Exchanging Step Matrix
temp_step = old_step; old_step = new_step; new_step = temp_step;
// Floyding
for (int i = 0; i < l; i++) {
for (int j = 0; j < l; j++) {
int w = old_step->$(i,k) + old_step->$(k,j);
if (w >= inf) w = inf;
if (w < old_step->$(i,j)) {
// WayPoint Setting
int nk = (i != k) ? this->waypoints->$(i, k) : k;
this->waypoints->s(nk, i, j);
} else w = old_step->$(i,j);
new_step->s (w, i, j);
}
}
}
После прохода алгоритма мы можем смело удалять использованные нами матрицы – они более не требуются.
delete old_step; delete new_step;
Следующим важнейшим шагом алгоритма является собственно построение пути. Для этой задачи мы используем созданную нами матрицу путевых точек. Как мы видим, матрица путевых точек позволяет нам легко отложить путь из любой точки в любую точку.
Обратим внимание, что при построении пути мы не используем бесконечный цикл. Причина проста. Мы можем гарантированно утверждать, что любой оптимальный и субоптимальный путь по графу из одной точки в другую всегда будет длиной меньше либо равен количеству вершин в графе. Доказать это несложно. Если предположить, что длина пути превышает количество точек, значит как минимум одну из точек пути мы посещаем более одного раза. Это означает, что из одной точки мы проделываем два пути, один из которых является петлёй, и возвращает нас назад в эту же точку, соответственно может быть исключён как лишний элемент пути.
path_t best_path;
best_path.type = -1;
best_path.weight = 0;
best_path.points = (int*) malloc (sizeof(int) * l);
for (int p = 0; p < l; p++) {
if (p) {
best_path.points[p] = this->waypoints->$(best_path.points[p-1], b);
best_path.weight += this->graph->$(best_path.points[p-1], best_path.points[p]);
if (p > 1) {
// Cathing Bad Path and Send
if (best_path.points[p] == best_path.points[p-2]) p = l-1;
}
} else {
best_path.points[0] = a;
}
// Finishing?
if (best_path.points[p] == b) {
best_path.type = 1;
best_path.length = p + 1;
break;
}
}
В случае если путь приводит нас в точку B, мы устанавливаем тип пути в единицу (оптимальный путь). В противном случае, если путь за конечное число шагов, меньшее количества вершин в графе, не привёл нас в точку B, значит, в графе имеются циклы, которые данный алгоритм не обрабатывает.
Далее, мы находим субоптимальные пути по идее алгоритма Йена. Мы рассмотрим определённое число вариантов пути, пытаясь на каждом из шагов пути выбрать не оптимальную точку, а вторую по оптимальности. Таким образом, мы можем максимум рассмотреть столько путей, сколько точек есть в оптимальном пути.
if (best_path.type != -1 && best_path.length > 2) {
int i_path_count = 0;
path_p i_paths = (path_p) malloc (sizeof(path_t) * (best_path.length - 2));
for (int i = 0; i < (best_path.length - 2); i++) {
i_paths[i].type = -1;
i_paths[i].length = 0;
i_paths[i].weight = 0;
i_paths[i].points = null;
}
Алгоритм построения субоптимальных путей отличается от алгоритма построения оптимального пути в одном из шагов, см. #2. На этом этапе мы проверяем, какой из путей (по номеру) мы анализируем, и совпадает ли номер пути с номером текущей точки. Если номер пути не совпадает, то построение ведётся как в предыдущем случае. В противном случае вместо оптимальной точки пути из матрицы путевых точек мы будем использовать другую точку, путь по которой будет отличаться от оптимального. Если такой точки не существует, то перейдём к следующему субоптимальному пути, так как субоптимального пути, отличающегося от оптимального этой точкой, не существует.
for (int k = 1; k < best_path.length - 1; k++) {
if (i_paths[i_path_count].points) free (i_paths[i_path_count].points);
i_paths[i_path_count].points = (int*) malloc (sizeof(int) * l);
for (int p = 0; p < l; p++) {
if (p == k) {
int n2p = (p > 1) ? i_paths[i_path_count].points[p-2] : -1;
int next_id = -1;
int next_wg = inf;
// Searching Next Way Poing not Best but Yet Good =)
for (int i = 0; i < l; i++) {
// i not this point, not previous point and not best point
if (i != i_paths[i_path_count].points[p-1] & i != n2p & i != this->waypoints->$(i_paths[i_path_count].points[p-1], b) ) {
if (this->graph->$(i_paths[i_path_count].points[p-1], i) < next_wg) {
next_id = i;
next_wg = this->graph->$(i_paths[i_path_count].points[p-1], i);
}
}
}
if (next_id != -1) {
i_paths[i_path_count].points[p] = next_id;
i_paths[i_path_count].weight += this->graph->$(i_paths[i_path_count].points[p-1], next_id);
} else p = l - 1; // Finishing, path is bad ...
} else if (p) {
// Simply Adding Next Way Point
i_paths[i_path_count].points[p] = this->waypoints->$(i_paths[i_path_count].points[p-1], b);
i_paths[i_path_count].weight += this->graph->$(i_paths[i_path_count].points[p-1], i_paths[i_path_count].points[p]);
if (p > 1) {
// Cathing Bad Path and Send
if (i_paths[i_path_count].points[p] == i_paths[i_path_count].points[p-2]) p = l-1;
}
} else {
// Starting
i_paths[i_path_count].points[0] = a;
}
// Finishing?
if (i_paths[i_path_count].points[p] == b) {
i_paths[i_path_count].type = 0;
i_paths[i_path_count].length = p + 1;
i_path_count += 1;
break;
}
// Bad Path Got?
if (p == l-1) {
free (i_paths[i_path_count].points);
i_paths[i_path_count].points = null;
}
}
}
После нахождения всех путей, мы можем перенести их в память решения. Мы отдельно выделяем место под окончательное решение в целях экономии памяти.
// Copying Paths to Result Array
this->paths = (path_p) malloc (sizeof(path_t) * (i_path_count + 1));
// Best Path
this->paths[0].type = 1;
this->paths[0].length = best_path.length;
this->paths[0].weight = best_path.weight;
this->paths[0].points = (int*) malloc (sizeof(int) * best_path.length);
for (int p = 0; p < best_path.length; p++) {
this->paths[0].points[p] = best_path.points[p];
}
// Sub Paths
for (int i = 0; i < i_path_count; i++) {
this->paths[i+1].type = i_paths[i].type;
this->paths[i+1].length = i_paths[i].length;
this->paths[i+1].weight = i_paths[i].weight;
this->paths[i+1].points = (int*) malloc (sizeof(int) * i_paths[i].length);
for (int p = 0; p < best_path.length; p++) {
this->paths[i+1].points[p] = i_paths[i].points[p];
}
free (i_paths[i].points);
}
free (i_paths);
this->path_count = i_path_count + 1;
} else if (best_path.type != -1) {
this->paths = (path_p) malloc (sizeof(path_t));
// Best Path
this->paths[0].type = 1;
this->paths[0].length = best_path.length;
this->paths[0].weight = best_path.weight;
this->paths[0].points = (int*) malloc (sizeof(int) * best_path.length);
for (int p = 0; p < best_path.length; p++) {
this->paths[0].points[p] = best_path.points[p];
}
this->path_count = 1;
}
После копирования путей в память решения, временная память очищается и функция возвращает количество найденных ей путей.
free (best_path.points); return this->path_count; }
Этим функция построения пути заканчивается. На выходе пользователь имеет количество путей. Таким образом, используя функцию path, передав ей в качестве параметра номер пути, мы получим информацию о каждом конкретном пути. При этом нулевой номер всегда имеет оптимальный путь.
Функция path возвращает ссылку на структуру пути, содержащуюся в решателе.
path_p c_floyd :: path (int id) {
if (this->path_count == 0 || id < 0 || id > this->path_count) {
return false;
} else return &this->paths[id];
}
Обратим внимание, что в случае сброса решателя (при любой операции с графами или запуске нового цикла решателя) данная ссылка становится неактуальной, так как сбрасывается и вся память решений. Поэтому, в случае использования данного решения многократно, после его получения стоит скопировать его в отдельную область памяти.
Класс floyd также содержит в себе ряд функций, которые мы используем для демонстрации решателя. Эти функции отвечают за распечатку пути, графа и матрицы путевых точек, их можно изучить напрямую в коде класса, рассматривать здесь их не имеет смысла из-за их очевидности и простоты реализации.
Демонстрация работы алгоритма
Для простой демонстрации работы алгоритма напишем небольшое консольное приложение. Оно выводит нам простое текстовое меню, запрашивающее у пользователя выбор действия. В зависимости от выбранного действия напрямую вызывается функция класса floyd с запрошенными у пользователя параметрами.
Возможны следующие варианты действий:
- Создать граф определённого размера со случайным весом рёбер.
- Отобразить матрицу весов в консоли.
- Отредактировать вес ребра в данной точке.
- Запустить решатель по алгоритмам Флойда и Йена.
- Показать пути, найденные в пункте 4.
- Показать матрицу путевых точек, используемую в пункте 4.
- Сохранить граф в файл graph.data.
- Загрузить ранее сохранённый файл из graph.data.
- Выйти из приложения.
Это приложение может использоваться для демонстрации работы библиотеки функций решателя по алгоритму Флойда. С небольшой доработкой эта библиотека может быть использована в реальных проектах.
Вывод
Рассмотренные алгоритмы могут легко применяться для нахождения оптимального и субоптимальных путей в графе. Используемые нами классы легко могут внедряться в существующие программные продукты на языке C++ и использоваться для решения задач в реальном времени. Реализации алгоритма Флойда и Иена могут, также, использоваться по отдельности, их код легко вычленяется из общего контекста.
Ссылки
Реализованные здесь алгоритмы описаны в следующих статьях:
- Wikipedia — http://ru.wikipedia.org/wiki/Алгоритм_Флойда_—_Уоршелла
- CurtisWiki — http://lib.custis.ru/index.php/Алгоритм_Флойда-Уоршолла
- http://khpi-iip.mipk.kharkiv.edu/library/datastr/book_sod/kgsu/din_0124.html
- Алгоритм Йена — http://algolist.manual.ru/maths/graphs/shortpath/yen.php
По этим ссылкам можно найти более детальное описание алгоритма, а также рассмотреть его реализации на различных языках программирования.
Исходные коды к этой статье Вы можете скачать здесь:
- Исходник – http://www.av13.ru/wp-content/uploads/2009/12/floyd-src.zip
- Реализация – http://www.av13.ru/wp-content/uploads/2009/12/floyd-exe.zip
- Отчёт — http://www.av13.ru/wp-content/uploads/2009/12/floyd-rtfm.zip
Создано в Microsoft Visual Studio 2008, лицензия кафедры АСОИиУ ФЭТ МГУ им. Н.П.Огарёва.
Автор
Автором данной статьи является Антон «AlterVision» Резниченко. Публикация статьи целиком или частично возможна только с разрешения автора.
9 декабря 2009 г. 18:50